「數學教改最大障礙，正是那些數學好的人」一張正方形圖片，看見學習的多樣性｜《人人都有數學腦》作者序

序言

友人邀請我去一家昂貴的餐廳，與英國最大的社群媒體平台執行長及其夫人共進晚餐。餐廳高級、奢華，是典型矽谷名流出入之地。入坐時，我有些惶恐不安，不知這個晚上會如何。這次餐敘是一位友人牽線的，他深知我對數學教學的熱情，也認識那位執行長的夫人，認為那位執行長將對我的志業有所幫助。過去幾年，我都在矽谷生活、工作，知道這種關係是矽谷結構的一部分，也是這個地區創新和生產力增長的一個重要原因。

一開始，我就察覺這次餐敘很不尋常，跟我參加過的任何一場宴會都大異其趣。做東的執行長就像我們這些受邀的賓客不在場似的，不是在講手機，就是在跟他公司的人員交談，忙著擬定工作計畫，還從公事包拿出一疊文件。不管有意或無意，這種行為使我們看起來就像閒雜人等。他的夫人見狀，面露尷尬，數度瞥向旁若無人的老公和他的工作團隊。直到上菜，執行長才不得不把文件收起來，放進公事包裡。飯吃到一半，他才注意到我的存在。他抬起頭來，盯著我，不以為然地說：「所以，你認為我們的數學教育應該改革？」接著，他喋喋不休地告訴我，他的數學有多好，在中學和大學時期拿下多少數學獎項。

這時，我察覺到這個人不好對付。多年來，我明知吃力不討好，還是一直努力想要改善數學教學—我知道數學教育改革最大的障礙，正是那些數學好的人。這些人通常認為數學教育不應該改變。他們認為，數學是很難的，他們數學成績優異，足以證明他們高人一等。但是如果你對我有點了解，就會發現我是這樣的人：我願意卯足全力幫助學生，幫他們解決真正的問題。於是，我打算採取我常用的一種策略，讓那位執行長瞧瞧一種不同的數學。我解釋說，神經科學家讓我們得以觀察大腦如何處理數學，尤其重要的一點是，在我們思索數學問題時，大腦哪些部位會變得活躍，特別是大腦的視覺路徑。接著，我問那位執行長是否願意看看一張有趣的數學圖片—我在遇見新朋友時常會這麼做。他同意了。我挑了我最喜歡的一張，也就是數學教育家露絲．帕克（Ruth Parker）繪製的圖片。

圖片來源：天下文化《人人都有數學腦》圖1.1  作者拿出一張圖片，上有正方形遞增的圖形，見圖1.1 和圖1.2

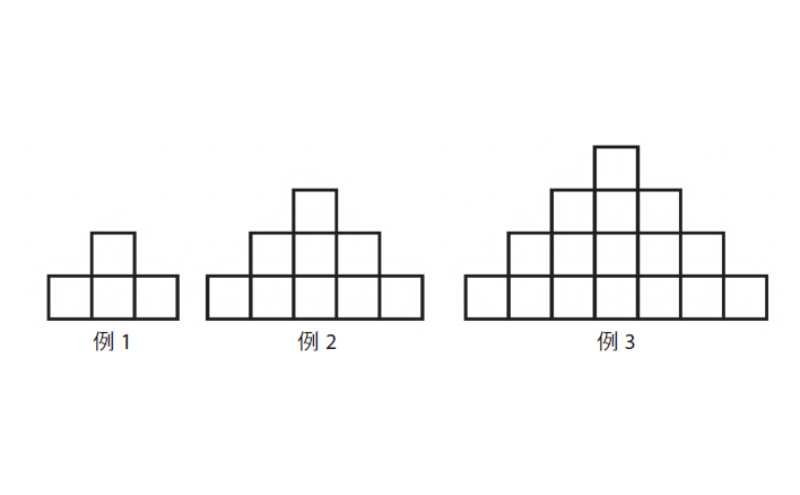
圖片來源：天下文化《人人都有數學腦》圖1.2  正方形遞增的模式

這樣的問題通常是用來幫助學生思考「模式增長」，進而使用代數符號來表示這種模式或關係。上數學課時，學生常會碰到這樣的問題：例 10 會有多少個正方形？例 100 呢？例 n 呢？這些都是好問題，但如果能激發數學多樣性的思維，則會是更好的問題。

通常，老師在課堂上會要求學生畫出一張數字表，然後盯著這張表格，直到看出其中規律。學生通常會注意到，表上的數字是有規律的，比方說拿其中一個例子來看（如例2），把這個數字加 1（變成 3），平方之後得到9，就是正方形的數目。透過這個加1 再平方的模式，就可求出任何一個例數的正方形數量。用代數來表示就是 (n+1)2。這種模式的表達式 (n+1)2 是一個二次函數。如果學生只是操弄數字和符號，不知其中關聯性或涵義，就會錯過了解數學函數的重要機會。在我的研究中，我改變提問的方式。雖然這只是小小的改變，意義卻很大。我不再問，每一例各有幾個正方形，而是問：你怎麼看這種模式的增長？多出來的正方形在哪裡？這些就是那晚我向執行長提出的問題。

每一例中的正方形數量

圖片來源：天下文化《人人都有數學腦》

執行長的回答讓我驚訝。他不是看不到增長的模式，他看得到，也能描述給我聽。他說，他看到每一列頂端多出來的正方形。其他人描述說，他看到正方形落在每一列頂端，就像「雨滴」從天而降。圖1.3 顯示這種「雨滴」型態和其他人看到的增長模式。

執行長分享他的看法之後，提出一個問題。我第一次聽到這樣的問題。他問道：「不是每一個人都這樣看嗎？」他的語氣流露出真正的疑惑。我沒告訴他，不是的，每一個人的看法不盡相同，我只是請同桌的每一個人分享他們的看法。於是， 每一個人輪流表達意見，結果發現每一個人都有不同的看法。執行長聽得目瞪口呆，好像從未想過看待數學問題的方式不只一種。他不可置信地搖搖頭，終於把注意力轉移到我們身上。

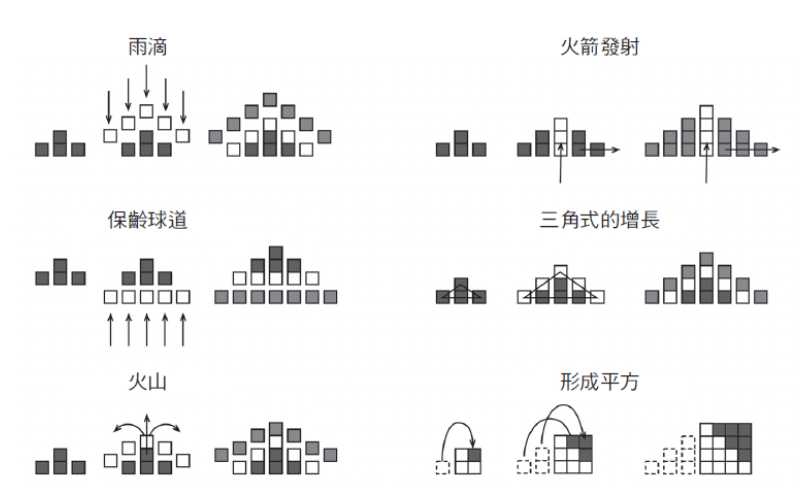
圖片來源：天下文化《人人都有數學腦》圖1.3  每一個人看到的模式各有不同，並描述自己看到的增長模式(n+1)2

用不同的方式問問題，打開眼界，用更廣闊的角度來看數學，這點很重要。如果學生只是用狹隘的眼光來解題，就會盯著那張數字表，企圖看出其中的規律，再用代數來表達，也許最後能看出這是 (n ＋ 1)2，還是不明白為什麼是這個二次函數， 也不知道這代表什麼意義。我們問學生，他們如何看出這種圖形模式，經過一番思索，對這個函數，就能有更深的了解，且能透過視覺，看出圖形模式的增長：後一例每一列頂端總是比前一例多一個正方形。最清楚的一例就是圖1.3 的最後一種。這就是為什麼我們用 (n ＋ 1)2 來描述這種增長模式。

我也在這場餐會中分享我非常熱中的一件事。這件事是根植於一件重要的神經研究，也就是數學多樣性的價值。「多樣性」（diversity）意謂不同、差異。在本書，我將用「數學多樣性」一詞，來涵蓋人的多樣性價值（種族、文化、社會等的不同），以及我們看待數學、學習數學的不同方式。我也將用「數學腦」（mathish）一詞來描述利用數學思考現實世界的一種思維方式。對學生來說，這將是一種非常有用的思考工具。如果能擁抱數學多樣性和數學腦的概念，無論一個人的教育程度、性別認同、種族或族裔為何，都可踏入廣大、豐富的數學天地。

研究顯示，學生的多樣性（student diversity）是合作、解決問題、展現同理心、學習成就等的關鍵。但研究也告訴我們，如果能用不同的眼光看數學這門學科，了解數學有許多不同的解法，就能增進學習成就，激發學習動機，讓學生覺得數學有趣，更喜歡數學。多樣性的兩個層面—人與人之間的差異和數學本身的差異—看似分開獨立，也能以美妙的方式結合，相互增強，相輔相成。我們鼓勵別人和自己有不同的想法並重視這點。可惜，大多數的人只知道狹隘的數學，認為數學都有標準答案。我們該揚棄這種思路，擁抱數學多樣性。

那天晚上，執行長看到的數學多樣性讓他非常震撼。學校和家庭往往缺乏這樣的多樣性，殘害個人與數學的關係，令人從小就討厭數學。有些人數學很好，但學的是狹隘的數學和標準答案。這樣的人，就算數學再高分，也無法掌握整個數學範疇和數學的力量。一個人若是接觸數學的多樣性，就能別具隻眼，以不同的眼光來看每一個與數字、空間和數據有關的情境。